Peluang, Permutasi, & Kombinasi Beserta Contoh Soal
Minggu, 12 Agustus 2018
Kaidah pencacahan
Ada tiga metode dalam kaidah pencacahan:
Aturan Pengisian Tempat yang Tersedia
Untuk memahami metode ini, kita dapat menjabarkannya menggunakan pasangan terurut. Jika suatu kejadian pertama dapat terjadi dalam 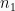 cara yang berbeda, kejadian kedua dapat terjadi dalam cara yang berbeda, dan seterusnya maka kejadian-kejadian itu secara berurutan dapat terjadi:
cara yang berbeda, kejadian kedua dapat terjadi dalam cara yang berbeda, dan seterusnya maka kejadian-kejadian itu secara berurutan dapat terjadi:
Sebagai ilustrasi: misalkan seorang pekerja memiliki 4 buah kemeja dan 2 buah dasi yang masing-masing mempunyai warna yang berbeda. Berapa pasangan warna kemeja dan dasi yang dapat dibuat? Jika himpunan kemeja adalah k = ( ) = 4 buah dan himpunan dasi adalah d = (
) = 4 buah dan himpunan dasi adalah d = ( ) = 2 buah. Sehingga dapat ditentukan bahwa:
) = 2 buah. Sehingga dapat ditentukan bahwa:
Permutasi
Permutasi adalah susunan berurutan dari semua atau sebagian elemen dari suatu himpunan. Dalam permutasi perlu dipahami terlebih dahulu terkait faktorial. Hasil kali bilangan bulat dari 1 sampai n adalah n! (dibaca : n faktorial) atau :
Contoh, 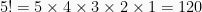 . Untuk menyelesaikan soal permutasi terdapat 4 metode yaitu:
. Untuk menyelesaikan soal permutasi terdapat 4 metode yaitu:
1. Permutasi dari elemen yang berbeda
Permutasi elemen dari elemen yang ada (setiap elemen berbeda) adalah susunan elemen itu dalam suatu urutan yang diperhatikan. Jika , ( ) permutasinya:
) permutasinya:  .
.
Sehingga jika 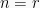 , permutasinya:
, permutasinya: 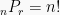 .
.
Sebagai ilustrasi: menyususn 3 elemen dari 3 huruf : a,b,c adalah a,b,c a,c,b b,c,a b,a,c c,a,b c,b,a dengan  . Sedangkan menyusun 2 elemen dari 3 huruf adalah dengan .
. Sedangkan menyusun 2 elemen dari 3 huruf adalah dengan . .
.
2. Permutasi dengan Beberapa elemen yang sama
Setiap unsur yang digunakan tidak boleh lebih dari satu kali. Banyak permutasi elemen n yang memuat elemen 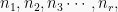 , dengan
, dengan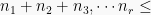 adalah:
adalah:
Sebagai ilustrasi: ada 3 bola basket dan 2 bola kasti. Jumlah cara menyusunnya:
3. Permutasi siklis
Rumus permutasi siklis biasanya digunakan untuk menghitung banyak cara yang dapat dibuat dari susunan melingkar. Rumusnya adalah
Sebagai ilustrasi: banyaknya cara 4 orang duduk melingkar dalam 1 meja adalah
4. Permutasi berulang
Permutasi berulang adalah permutasi yang dalam penyusunannya urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali (berulang). Banyaknya permutasi ini adalah
Sedangkan untuk rumus permutasi yang tidak boleh ditulis berulang adalah
Kombinasi
Kombinasi adalah pengelompokan dari semua atau sebagian elemen dari suatu himpunan tanpa memperhatikan urutan susunan pemilihannya. Banyaknya kombinasi adalah :
Sebagai ilustrasi : kombinasi 2 elemen dari 3 huruf a,b,c adalah ab, ac, bc . Sedangkan ba, ca, cb tidak termasuk hitungan karena pada kombinasi ab=ba, ac=ca, bc=cb. Banyak kombinasi adalah :
Binom Newton
Binom Newton berhubungan dengan bentuk  . Dimana suku ke-r dari bentuk tersebut adalah :
. Dimana suku ke-r dari bentuk tersebut adalah :
Suku ke – r = 
Sebagai ilustrasi: koefisien 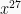 dari
dari 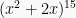 adalah:
adalah:
Agar x berpangkat 27 dibuat:
Sehingga:
suku ke – 4 = 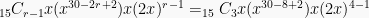 .
.
Koefisiennya: 3640
Peluang Suatu Kejadian
Peluang atau probabilitas adalah kemungkinan sebuah kejadian dapat terjadi. Percobaan merupakan suatu proses yang dilakukan untuk kemudian memperoleh suatu hasil pengukuran, perhitungan, ataupun pengamatan. Himpunan dari semua hasil yang mungkin dari suatu percobaan disebut ruang sampel (S). Sehingga kejadian atau peristiwa merupakan himpunan bagian dari ruang sampel atau bagian dari hasil percobaan yang diinginkan.
Nilai probalitas antara 0 – 1. Kejadian yang mempunyai nilai probabilitas 0 adalah kejadian yang mustahil terjadi atau tidak mungkin terjadi. Sedangkan kejadian yang mempunyai nilai probalilitas 1 adalah kejadian yang pasti terjadi atau kejadian yang sudah terjadi.
Peluang atau probabilitas suatu kejadian A dapat terjadi dengan k dan mungkin hasil terjadi m cara sebagai:
Frekuensi harapan suatu kejadian adalah hasil kali banyaknya percobaan dengan peluang kejadian yang akan terjadi dalam suatu percobaan atau:
Peluang Kejadian Majemuk
Peluang Gabungan Dua Kejadian
Dua buah kejadian A dan B dikatakan gabungan dua kejadian jika kejadian A dan B kejadian dapat terjadi bersamaan sehingga 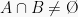 dan menghasilkan rumus:
dan menghasilkan rumus:

Peluang Gabungan Dua Kejadian yang Saling Lepas
Dua buah kejadian A dan B dikatakan gabungan dua kejadian saling lepas jika kejadian A dan B tidak mungkin terjadi bersamaan. Sehingga 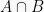 dan menghasilkan rumus:
dan menghasilkan rumus:

Peluang Komplemen suatu Kejadian
Kejadian merupakan komplemen/ kebalikan A sehingga A danA’ merupakan kejadian saling lepas, maka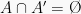 . Sehingga menghasilkan rumus:
. Sehingga menghasilkan rumus:

Peluang Kejadian Bersyarat
Dua kejadian disebut kejadian bersyarat jika munculnya kejadian pertama A mempengaruhi peluang munculnya kejadian kedua B. Maka peluang terjadinya kejadian B yang dipengaruhi oleh kejadian A ditulis dengan  . Bila
. Bila  adalah peluang terjadinya A dan B , maka
adalah peluang terjadinya A dan B , maka
Contoh Soal Peluang dan Pembahasan
Contoh Soal 1
Dalam sebuah kotak berisi 7 bola merah dan 5 bola putih. Dari kota itu diambil 3 bola sekaligus. Peluang terambil sekurang-kurangnya 1 bola putih adalah
Pembahasan 1:
Karena harus terambil sekurang-kurangnya 1 bola putih maka peluang tidak terambilnya bola putih tidak termasuk itungan sehingga:
Contoh Soal 2
Tentukanlah nilai n yang memenuhi persamaan
Pembahasan 2:
Contoh Soal 3
Berapa banyak urutan yang dapat terjadi jika 5 bendera yang berwarna putih, merah, hijau, kuning, dan biru dipancang pada tiang-tiang dalam satu baris, dengan bendera putih selalu berada di salah satu ujung.
Pembahasan 3:
Karena bendera putih dipancang dalam salah satu ujung maka dengan 2 cara, sisa 4 bendera dapat diatur dalam  cara, sehingga:
cara, sehingga:
Jumlah urutan 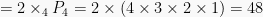 urutan.
urutan.
