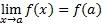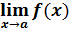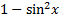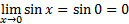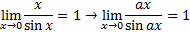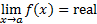Limit ( Materi Matematika SMA )

Definisi dan Pengertian Limit

1.1. Definisi Limit

Berikut adalah definisi limit menurut Austin Louis Cauchy:

Sebuah fungsi f(x) mempunyai jika dan hanya jika untuk sembarang bilangan real  maka terdapat bilangan real  sedemikian hingga memenuhi:

 maka 

1.2. Pengertian Limit

Supaya lebih memahami pengertian limit, berikut disajikan contoh:

Perhatikan fungsi aljabar

 

Agar fungsi f(x) terdefinisi, nilai x dibatasi yaitu x ≠ 1. Jika batas nilai x tersebut didekati, akan diperoleh hasil bahwa nilai fungsi mendekati 3 

Pada kasus seperti di atas dikatakan limit  untuk x mendekati 1 adalah 3, ditulis: .

2. Limit Fungsi

 artinya nilai x mendekati nilai a (tetapi x ≠ a) maka f(x) mendekati nilai L.

2.1. Sifat-Sifat Teorema Limit Fungsi

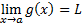
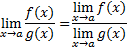
Jika  dan maka: 

, untuk 

Jika 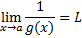 maka: untuk L ≠ 0

2.2. Menentukan Nilai dari Suatu 

Jika f(a) = k maka Jika  maka Jika  maka Jika  atau bentuk tertentu  maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3).

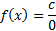
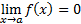
2.3. Limit Fungsi Tak Terhingga

 Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)

 Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x)

 Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x)

3. Limit Fungsi Aljabar

3.1. Limit Fungsi Aljabar Berhingga

Jika f(a)=C, maka nilai 

Jika , maka nilai 

Jika , maka nilai disederhanakan dulu menjadi bentuk 1, 2, atau 3

3.2. Limit Fungsi Aljabar Tak Terhingga

Menentukan nilai  atau :

Jika n = m maka Jika n > m maka Jka n < m maka 

4. Limit Fungsi Trigonometri

Untuk menghitung nilai limit fungsi trigonometri digunakan rumus-rumus berikut:

Kemudian, secara umum dapat menggunakan langkah-langkah cepat seperti di bawah ini:

Jika terdapat fungsi cos maka ubahlah ke dalam bentuk sebagai berikut:

cos x diubah menjadi  diubah menjadi 

Berikut adalah sifat-sifat teorema limit fungsi geometri lainnya:

5. Kontinuitas

Suatu fungsi kontinu di x = a jika:

f(a) real

Sumber : https://hedisasrawan.blogspot.co.id/2014/12/limit-fungsi-materi-sma-xi-ipa-semester.html?m=1

Baca Artikel Terkait: